Leetcode
本文最后更新于 2024-04-15,文章内容可能已经过时。
LeetCode
主要记录自己刷leetcode的一些记录和思考.
1.两数之和
1.1 自己做的:
直接暴力求解:
class Solution {
public int[] twoSum(int[] nums, int target) {
for(int i=0;i<nums.length;i++){
for(int j=0;j<nums.length;j++){
if(nums[i]+nums[j]==target&&i!=j){
return new int[]{i, j};
}
}
}
return new int[0];
}
}1.2 更好的方法:
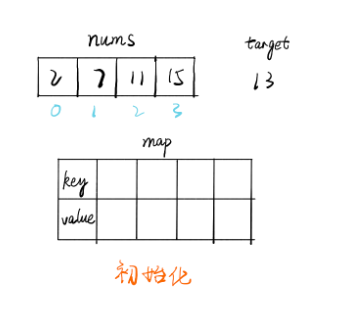
建立一个hash表,key为值,value为索引.
每次添加数据时,先看target-这个数据的值 这个key是否存在,如果不存在则添加数据,存在就直接返回结果.
用更多的数据存储换来更快的速度.
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i< nums.length; i++) {
if(map.containsKey(target - nums[i])) {
return new int[] {map.get(target-nums[i]),i};
}
map.put(nums[i], i);
}
throw new IllegalArgumentException("No two sum solution");
}
}2.移动零:
1.1 自己做的:
没写代码.只有思路.
一个指针从最前方开始,一个指针从最后方开始.
当左指针指向0,右指针指向第一个非0元素时:
将左指针右边所有的元素减一,最后剩下的那个元素设置为0.
直到两个指针相遇为止.
1.2 题解:
感觉和自己做的差不多.只不过两个指针是从同一个方向开始.
class Solution {
public void moveZeroes(int[] nums) {
int n = nums.length, left = 0, right = 0;
while (right < n) {
if (nums[right] != 0) {
swap(nums, left, right);
left++;
}
right++;
}
}
public void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}简单来说是把0一点一点的移到最右边去.
使用双指针,左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。
右指针不断向右移动,每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移。
注意到以下性质:
左指针左边均为非零数;
右指针左边直到左指针处均为零。
因此每次交换,都是将左指针的零与右指针的非零数交换,且非零数的相对顺序并未改变。
3.相交链表:
1.1 自己做的:
采用双指针思路.
两个指针均从链表头开始移动,每个指针移动一次,都比较当前两个值.
但是这样有个问题,就是当两个链表相差的节点数大于等于2时就无法完成了.
1.2 题解:
使用双指针的方法解决.
简单来说,就是首先遍历链表,找到哪个是更长的,然后两个都从短的那一端开始,相互进入遍历.
以下是根据题解 自己写的代码.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode pA=headA;
ListNode pB=headB;
int i=0;
int j=0;
while(headA!=null){
i++;
headA=headA.next;
}
while(headB!=null){
j++;
headB=headB.next;
}
int m;
int n = 0;
if(i>j){
m=i-j;
n=1;
}else{
m=j-i;
n=2;
}
headA=pA;
headB=pB;
if(n==1){
for(i=0;i<m;i++){
headA=headA.next;
}
}
if(n==2){
for(i=0;i<m;i++){
headB=headB.next;
}
}
while(headA!=headB){
headA=headA.next;
headB=headB.next;
if(headA==null){
return null;
}
if(headB==null){
return null;
}
}
return headA;
}
}
4.盛最多水的容器:
需要采用头尾双指针的方式。
注意只有移动矮的才有用。
func maxArea(height []int) int {
var right, left, result, d int
left = 0
right = len(height) - 1
if height[right] < height[left] {
result = (right - left) * height[right]
} else {
result = (right - left) * height[left]
}
for right != left {
//移动
if height[right] < height[left] {
right -= 1
} else {
left += 1
}
//计算面积
if height[right] < height[left] {
d = (right - left) * height[right]
if d > result {
result = d
}
} else {
d = (right - left) * height[left]
if d > result {
result = d
}
}
}
return result
}5.最大子数组和:
这道题的官方解法和常规的动态规划有点不同。
定义的递归子问题和原问题不同,而是再多一遍遍历去做的。
这样不是很好,可以这样做:
dp[i] [j]定义为前i个数构成的数组的最大值,j表示包不包含最后一个数。
6.爬楼梯:
最简单的dp之一。
7.杨辉三角:
同样是简单的dp,一维,不需要太多的操作。
8.打家劫舍:
一维的dp,但是在写优化子结构的时候,需要考虑dp[i-1]和dp[i-2] 以后写不出来的话可以考虑是否需要再更前一个的dp状态。
9.完全平方数:
纯恶心人题,优化子结构想不出来,看答案也看不懂。
10.买卖股票的最佳时机:
二维的动态规划。需要是否持有股票这一个状态。
11.跳跃游戏:
边界条件的判断需要优化。属于投机取巧的简单做法。
func canJump(nums []int) bool {
length := len(nums)
if length ==1 {
return true
}
tag := 0
for i:=0;i<length;i++{
if i == length-1 {
break
}
if nums[i]>0 {
continue
}
if nums[i]==0 {
for j:=i-1;j>=0;j--{
if nums[j]>i-j{
if j+nums[j] >= length-1{
tag = 1
break
}
if nums[j+nums[j]]>0 {
tag = 1
}
if nums[j+nums[j]-1]>0 {
tag = 1
}
if nums[j+nums[j]-2]>0 {
tag = 1
}
}
}
if tag == 1{
tag = 0
continue
}else {
return false
}
}
}
return true
}12. pow(x, n):
可能会超时,注意乘方的优化,和正数负数的考虑。
func myPow(x float64, n int) float64 {
var res float64
var tag float64
var tag2 int
tag = 1.0
if n<0 {
n = n*(-1)
tag2 =1
}
for n>2 {
if n%2 ==0 {
n = n/2
x = x*x
continue
}
if n%2 == 1{
n = n-1
tag = tag * x
continue
}
}
res = x
if tag2 == 1 {
for i:=0;i<n-1;i++ {
res = res * x
}
return 1.0/(res*tag)
}
if n>0 {
for i:=0;i<n-1;i++ {
res = res * x
}
return res*tag
}
return 1
}难得的击败了百分百的用户:
13.有效的括号:
使用栈的思想来解决这个处理数组里面相邻的数字的问题。
判断当前读取字符和栈顶字符是否相同,如果相同则消掉,如果不相同则压入栈,最后判断栈内的元素个数即可。
14.最小路径和:
dp[i][j]\textit{dp}[i][j]dp[i][j] 表示从左上角出发到 (i,j)(i,j)(i,j) 位置的最小路径和。显然,dp[0][0]=grid[0][0]\textit{dp}[0][0]=\textit{grid}[0][0]dp[0][0]=grid[0][0]。对于 dp\textit{dp}dp 中的其余元素,通过以下状态转移方程计算元素值。
当 i>0i>0i>0 且 j=0j=0j=0 时,dp[i][0]=dp[i−1][0]+grid[i][0]\textit{dp}[i][0]=\textit{dp}[i-1][0]+\textit{grid}[i][0]dp[i][0]=dp[i−1][0]+grid[i][0]。
当 i=0i=0i=0 且 j>0j>0j>0 时,dp[0][j]=dp[0][j−1]+grid[0][j]\textit{dp}[0][j]=\textit{dp}[0][j-1]+\textit{grid}[0][j]dp[0][j]=dp[0][j−1]+grid[0][j]。
当 i>0i>0i>0 且 j>0j>0j>0 时,dp[i][j]=min(dp[i−1][j],dp[i][j−1])+grid[i][j]\textit{dp}[i][j]=\min(\textit{dp}[i-1][j],\textit{dp}[i][j-1])+\textit{grid}[i][j]dp[i][j]=min(dp[i−1][j],dp[i][j−1])+grid[i][j]。15.只出现一次的数字:
异或。
不使用辅助数组的话,使用哈希表解决问题。
16.反转链表:
16.1 数据结构:
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/16.2 定义变量:
按照一定的思路遍历这些变量。
当前 curr
前 pre
后 next
16.3 代码:
func reverseList(head *ListNode) *ListNode {
var curr,pre,next *ListNode
curr = head
for curr != nil {
//保存下一个节点
next = curr.Next
//修改
curr.Next = pre
//重置pre 为curr
pre = curr
//修改当前
curr = next
}
return pre
}17.回文链表:
具体思路是把链表遍历一遍,
func isPalindrome(head *ListNode) bool {
vals := []int{}
for ; head != nil; head = head.Next {
vals = append(vals, head.Val)
}
n := len(vals)
for i, v := range vals[:n/2] {
if v != vals[n-1-i] {
return false
}
}
return true
}18.环形链表:
两种方式:
一是使用存储链表节点,使用哈希做判断的方式。
二是快慢指针,如果慢指针能追上快指针,就证明有环。
如果不能追上就没环。
19.阶乘后的零:
考虑这个数能被5整除多少次。
20.寻找峰值:
21.不同路径二:
dp 表示到某一个格子的路径。
22.最大正方形:
dp[i] [j]
表示到当前位置,以当前位置为结尾的正方形的最大面积。

